Synaptic Numerology

The Keepers, like many of their adopted cultures, believe that certain numbers are auspicious and others unlucky. In the case of the Keepers, the distinction is easily grounded in a simple principle. Those numbers that signify the possibility of equal repetition and division are an anathema, for example the number four, upon which the Cartesian Grid depends. The Keepers believe this vision of the infinite - the infinite that is far away - is the crucial lie, by which we remain ignorant of the Synapse.

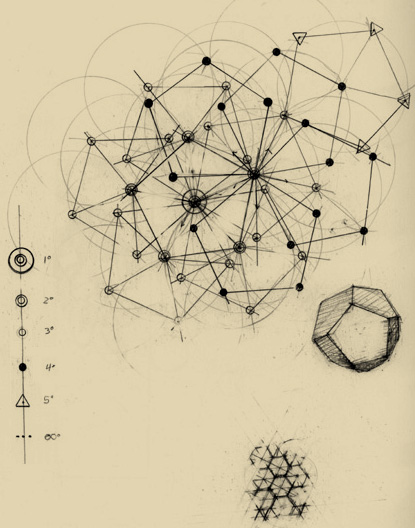
On other hand, those numbers that fold easily into recursion, infinitesimal spirals, or nested infinities, are considered holy, being reflections of the Geometry of the Synapse. A revered number is Five, whose pentagonal form could never tile a floor, but which lends itself to radial symmetries emerging from on a central point outwards in fractal crescendos of self-similarity.

The Labyrinth of the Codex is sometimes represented as a single point, around which five points in the shape of a pentagon are evenly spaced, representing the five paths of reference that always radiate from a single codex. Each of these five points has its own pentagon of reference in turn. If there were six, not five points, a repeating pattern of hexagonal tiles would quickly emerge. With each generation of five-fold symmetry however, the pattern rapidly spirals into an increasingly ornate pattern of connections whose only point of symmetry lies at the origin, a point of proiminence which can nonetheless be held by any Codex, depending on where one starts.

This spiralling pattern underlies the arrangement of objects in many Synapse Myths. The trees in the Memory Forest adhere to a five-fold Symmetry. The wanderer, at every tree always ends up - impossibly - in the hub of a great wheel of trees, rather than merely another identical tile on an endless floor.

It should be noted that this same generative pattern, when allowed to work in three dimensions instead of two, neatly conforms to the shape of a perfect icosohedron, and its geometric reciprocal, the dodecahedron. A Keeper's proverb: "One worlds's chaos is another's order."

show